Le courant
alternatif
Définition Déphasage Cosinus Impédance
Puissance
Rendement
Résonnance
![]() Un mouvement pendulaire d'amplitude constante
enregistré à vitesse constante donne une courbe
trigonométrique : la sinusoïde.
Un mouvement pendulaire d'amplitude constante
enregistré à vitesse constante donne une courbe
trigonométrique : la sinusoïde.
Un courant électrique dont l'intensité I et la
tension U varient périodiquement en fonction du temps de
façon sinusoïdale est appelé : courant alternatif.
II est caractérisé:
2
2
- Par
sa période T = ---- = 2
f = ----.
T
- Par son amplitude : valeurs
maximales : I max et U max.
- La pulsation est = 2
f, l'angle décrit par le secteur
trigonométrique
après le temps t en
seconde est:
=
t

- Les valeurs Instantanées sont:
It = Imax
sin t = Imax .sin
Ut
= Umax sin t = Umax.sin
- Les valeurs efficaces données généralement par
les instruments de mesure sont:
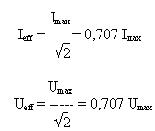
- Les valeurs
moyennes sont:
2 Imax
Imoy
= ------ = 0,6366 Imax
![]()
2Umax
Umoy
= ------- = 0,6366 Umax
![]()
La relation entre U et I est
fonction de la loi d'Ohm
Umax = Imax . R
Ueff
= Ieff .R.
![]() Déphasage
Déphasage
Une résistance pure ne crée pas de déphasage
entre la tension et l'intensité dans un circuit
alimenté en courant alternatif. Lorsqu'une d.d.p.
alternative U sin t est
appliquée aux bornes d'un circuit et que le courant
résultant est égal à:
I = Imax.Sin( t ±
![]() )
)

![]() est la différence de phase entre la
tension et le courant, c'est le déphasage; il peut être
positif ou négatif.
est la différence de phase entre la
tension et le courant, c'est le déphasage; il peut être
positif ou négatif.
Dans un circuit inductif, ![]() est positif : I est
déphasé en arrière sur U.
est positif : I est
déphasé en arrière sur U.
Dans un circuit capacitif, ![]() est négatif : I est
déphasé en avant sur U.
est négatif : I est
déphasé en avant sur U.
Lorsqu'un courant alternatif
parcourt une résistance, la tension et l'intensité
varient simultanément ; leurs effets sont conjugués.
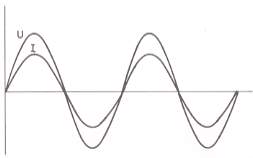 La puissance dans
une résistance est donc:
La puissance dans
une résistance est donc: Toute l'énergie est utilisée.
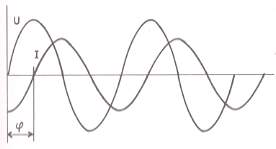
Si ce courant alternatif parcourt une bobine, le champ
magnétique variable (provoqué par le courant) induit
dans cette même bobine un courant alternatif secondaire
qui obéit â la loi de LENZ.
L'intensité est en retard, sur la tension. Elles ne sont
plus en phase, on dit qu'il y a déphasage. Les effets de
la tension et de l'intensité ne se conjugant plus, la
puissance demandée au réseau est supérieure â celle
nécessaire au travail. I1 y a perte d'énergie.
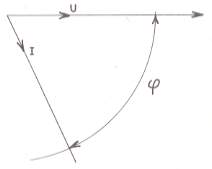
On appelle facteur de puissance le cosinus ![]() de l'angle de déphasage formé par les vecteurs
d.d.p et intensité.
de l'angle de déphasage formé par les vecteurs
d.d.p et intensité.
R est une résistance pure dans un circuit continu ou alternatif. Z est la résistance d'un circuit alternatif affecté d'un déphasage (impédance):
![]()
1
X =
réactance en ohms = L - ----
C
1
L = réactance inductive et ---- = réactance
capacitive (en ohms).
C
La loi d'Ohm en alternatif s'applique en remplaçant R par Z
Umax = ZImax, Veff
= ZIeff.
Dans un
circuit sans déphasage (![]() = 0)
= 0)
Umax . Imax
P = Ueff . Ieff,
P = -------------
2
Si l'on considère les formules de base:
a) P = UI où P,
la puissance cherchée est en Watt
U, la D.D.P. (différence de
Potentiel en Volt,) aux bornes de la résistance, et
I , l'intensité du courant
traversant le circuit;
b) U = RI
1ère loi d'ohm où U = D.D.P., R = résistance en ohm et I l'intensité en ampères dans le
circuit;
On peut donc déduire de ces deux
formules:
P = Ueff. Ieff
. Cos .![]()
cos![]() = facteur de
puissance, c'est le cosinus de l'angle de déphasage R/Z.
= facteur de
puissance, c'est le cosinus de l'angle de déphasage R/Z.
- Puissance apparente
Pa ou S = U.I en VA (volt-ampère).
- Puissance active P
= U.I cos![]() en W (watt).
en W (watt).
- Puissance réactive Pr ou Q = U.I
sin ![]() en var.
en var.
- Intensité wattée I
= I cos![]() (A).
(A).
- Intensité déwattée I
= I sin![]() (A).
(A).
- F.é.m. énergétique E
= E cos![]() (V).
(V).
- F.é.m. en quadrature E
= E sin![]() (V).
(V).
Tableau des impédances, déphasages
et puissance en fonction des éléments d'un circuit.


RENDEMENT d'UN MOTEUR ÉLECTRIQUE
DÉFINITION :
le rendement d'un moteur électrique est le rapport de la puissance qu'il développe, sur la puissance absorbée.
l Ch = 736 watts
1)
Exemple:
Un moteur
fonctionnant sous 220 V et consommant une intensité de 8 A
développe une puissance réelle de 2 Ch.
- Quel est son rendement ?
Réponse: Puissance absorbée: P = UI = 220 x 8 = 1 760 W
Puissance réelle: 736 x 2 = 1 472 W
Rendement ( Rt ): 1472 = 0,83 ou
83 %
1760
2) Exemple
Quelle est la puissance réelle d'un moteur qui fonctionne sous 220 V, 10 A, avec un rendement de 72 %
Réponse:
Puissance absorbée: P = UI x 220 x 10 = 2200 W
Puissance réelle: 2200 x 72 ou 2200 x 0,72 =
1584 W
100
Puissance réelle en Ch: 1584 = 2,15 Ch
736
![]() CIRCUIT OSCILLANT
SÉRIE
CIRCUIT OSCILLANT
SÉRIE
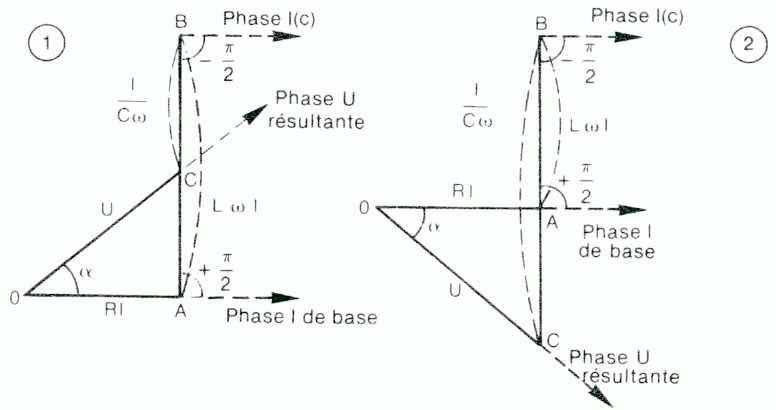
Impédance:![]()
Trois cas possibles : (sens trigonométrique inverse des aiguilles d'une montre).
(1) ![]() est plus grand que
est plus grand que![]() , le circuit est inductif, I est déphasé en
arrière sur la tension.
, le circuit est inductif, I est déphasé en
arrière sur la tension.
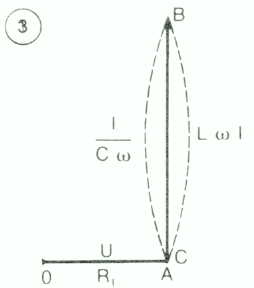
(2) ![]() est plus petit que
est plus petit que ![]() , le circuit est
capacitif, I est déphasé en avant sur la tension.
, le circuit est
capacitif, I est déphasé en avant sur la tension.
(3)![]() est égal
à
est égal
à ![]() il n'y a
plus de déphasage, le circuit est en résonance série : Z =
R; I est
maximal.
il n'y a
plus de déphasage, le circuit est en résonance série : Z =
R; I est
maximal.
Par contre les tensions aux bornes de L et C sont:
![]() I et
I et ![]()
qui peuvent être beaucoup plus grandes que RI.
Le coefficient de
surtension, ou l'indice de qualité Q est:
![]() pour la
self-induction et
pour la
self-induction et ![]() pour la
capacité.
pour la
capacité.
C'est le nombre de fois qu'il faut multiplier la tension de la source U pour obtenir la tension aux bornes de la self-induction ou aux bornes de la capacité.
![]() CIRCUIT
OSCILLANT PARALLELE
CIRCUIT
OSCILLANT PARALLELE
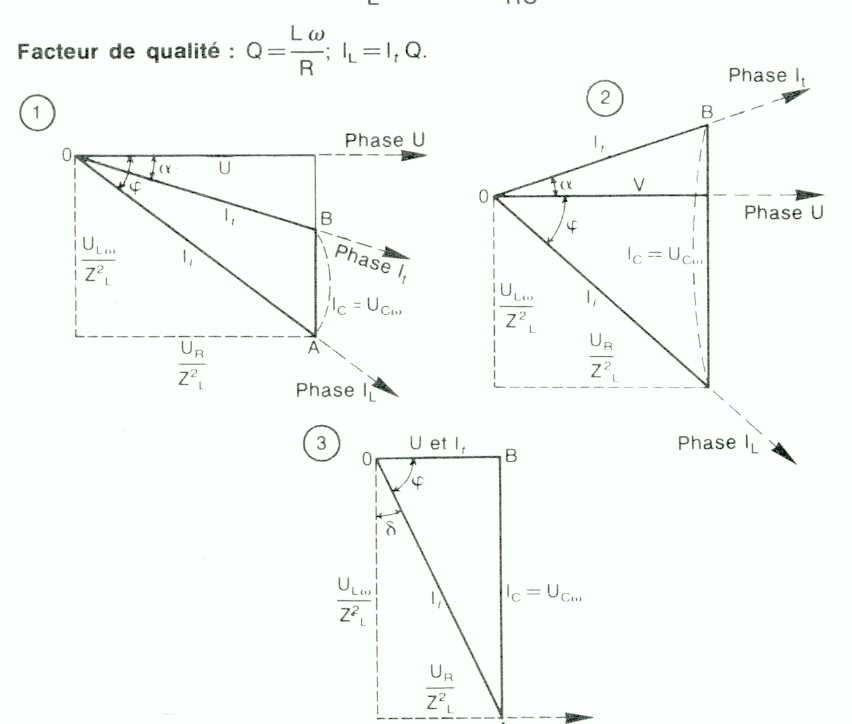
L et R sont en parallèle sur
C, la résolution graphique s'opère en raisonnant sur les
intensités qui parcourent les deux branches pour en tirer
l'intensité totale.
Si U est la tension de la
source, Ic = UC déphasée de 90°
en avant sur U, l'intensité dans la bobine et dans la
résistance:
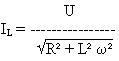
![]() ; IL est déphasée en
arrière sur U d'un angle
; IL est déphasée en
arrière sur U d'un angle ![]() donné par
donné par
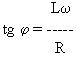
On trace une droite
horizontale U origine des déphasages. A partir de O on
porte le vecteur IL déphasé en arrière d'un
angle ![]() (A). On trace
(A). On trace ![]() perpendiculaire à
l'horizontale U, déphasé de 90° en avant, proportionnel à
Ic. On obtient
perpendiculaire à
l'horizontale U, déphasé de 90° en avant, proportionnel à
Ic. On obtient ![]() proportionnel à It et déphasé de
l'angle
proportionnel à It et déphasé de
l'angle par rapport à U.
Trois cas possibles:
(1) ![]() est
plus grand que UC
est
plus grand que UC , le circuit est inductif, It est
déphasé en arrière sur U.
(2) ![]() est plus petit que UC
est plus petit que UC , le circuit est capacitif, It est
déphasé en avant sur U.
(3) ![]() est égal à UC
est égal à UC , le circuit est en
résonance parallèle.
It
est en phase avec U, le courant dans le circuit est le
plus faible. Si R est très petit, on peut le négliger.
La condition de résonance devient:

U
l'impédance à la résonance est : ZR = ----- .
It
Si R
n'est pas négligeable:
RUC
L
It
= ------ et ZR = -----.
L
RC
Ici le facteur Q multiplie le courant dans le circuit pour trouver le courant dans les éléments. L'impédance du circuit est élevée à la résonance; le courant dans L et C est grand, tandis que le courant total est faible.
L'angle de perte
du circuit est : 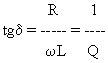
Plus la qualité du circuit est grande, plus l'angle de
perte est petit.
![]() FRÉQUENCE DE
RÉSONANCE
FRÉQUENCE DE
RÉSONANCE
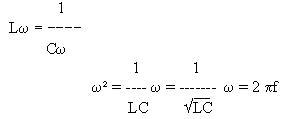
 (formule de
Thomson).
(formule de
Thomson).
![]() PARALLELE
RÉSUMÉ ENTRE LES DEUX RÉSONANCES
PARALLELE
RÉSUMÉ ENTRE LES DEUX RÉSONANCES

Accueil
Retour Haut de la page